斐波那契数列的四种生成方式

2016-06-01

简介

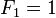
费波那契数列（意大利语：Successione di Fibonacci），又译费波拿契数、斐波那契数列、费氏数列、黄金分割数列。在数学上，费波那契数列是以递归的方法来定义： $F_0=0$ $F_1=1$ $F_n = F_{n-1}+ F_{n-2}$ （n≧2）用文字来说，就是费波那契数列由0和1开始，之后的费波那契系数就由之前的两数相加。首几个费波那契系数是（ A000045）： 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…… 特别指出：0不是第一项，而是第零项。来自维基百科

解法1: 递归法

def fib1(n):
    """递归法， 复杂度高"""
    if n==1 or n==2:
        return 1
    else:
        return fib1(n-1)+fib1(n-2)

解法2: 迭代法

def fib2(n):
    """迭代法， 复杂度一般"""
    if n==1 or n==2:
        return 1
    first = 1
    second = 1
    temp = 0
    for i in xrange(n-2):
        temp = first + second
        first, second = second, temp
    return temp

fibs = [0, 1]numZS = input('How many Fibonacci numbers do you want? ')
for i in range(numZS-2): fibs.append(fibs[-2] + fibs[-1])
print fibs

解法3: 通项公式法

def fib3(n):
    """通项法， 复杂度极低， 但在计算机上有精度问题"""
    import math
    sqrt_5 = math.sqrt(5)
    return int(sqrt_5/5.0*(((1+sqrt_5)/2.0)**n-((1-sqrt_5)/2.0)**n))

解法4: 矩阵乘法

def fib4(n):

    """矩阵乘法， 复杂度低， 无精度问题， Ok"""
    t = [[1, 1], [1, 0]]
    two(n, t)
    return t[0][0]

def two(n, t):
    """计算2维矩阵的辅助函数"""
    if n == 1:
        n = 2
    for i in range(n-2):
        t[0][0], t[0][1], t[1][0], t[1][1] = t[0][0]+t[0][1], t[0][0], t[1][0]+t[1][1], t[1][0]

Blog

Opinion

Project

OverAPI